Miller index

“Miller index” is a set of three indices h, k, l that identify the atomic plane (lattice plane) of a crystal. When considering the atomic plane closest to the origin without passing through the origin, let u, v and w be the coordinates intersecting the crystal axes a, b and c, and the lengths of the unit cell of the crystal be a, b and c, Miller index of the plane is given by a/u, b/v, c/w. If any of the ratios a/u, b/v, c/w takes a fractional number, the Miller index is expressed by rewritten with integral numbers.
In the example shown in Fig. 1, the coordinates at which the atomic plane intersects the a, b, c axes are u = a/4, v = b/1, w = c/2. Since a/u = 4, b/v = 1, c/w = 2, the Miller index is h=4, k=1, l=2. That is, the lattice plane shown in the figure is the (412) plane. When expressing a plane in a crystal, the index is enclosed in parentheses. (When expressing a direction in a crystal, the index is enclosed in square brackets [ ])

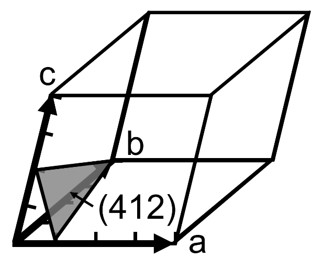
Fig. 1. Miller index.

Related Term(s)