Fourier transform

A method that transforms a function of certain variables into a function of the variables conjugate to the certain variables. For example, "Fourier transform" is used for light or sound as a function of time to express it as a function of frequency (spectral analysis), or for scattered waves from an object or a crystal potential as a function of position to transform it into a diffraction pattern or crystal structure factors as a function of wavenumber.

The imaging lens system of a TEM can be considered as a system in which scattered waves from an object or a crystal potential are Fourier transformed into a diffraction pattern and subsequently inverse Fourier transformed to an image of the object, where the assumption of Fraunhofer diffraction is applied.

Here, ψ(r) stands for the scattered waves from the specimen, being a function of the real space r, and Ψ(k) for the diffracted waves formed on the back focal plane of the imaging lens, being a function of the reciprocal space k [1/m]. The first equation expresses Fourier transform. That is, the scattered waves ψ(r) produced by the specimen are transformed to a diffraction pattern Ψ(k). The second equation expresses inverse Fourier transform. That is, the diffraction pattern Ψ(k) is transformed to a specimen’s image ψ(r).

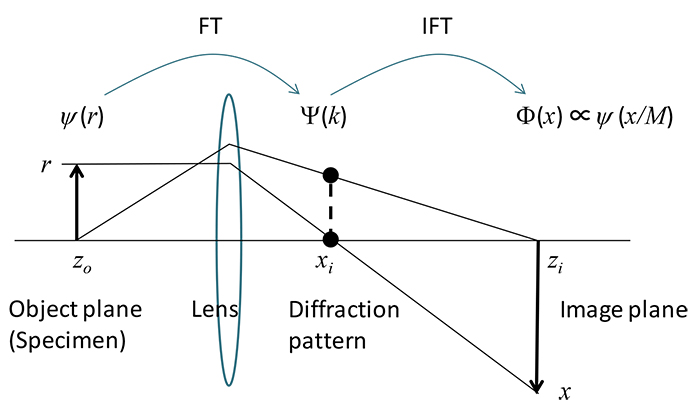
Fig. 1 TEM imaging by a lens (image and diffraction pattern)
The imaging process of a transmission electron microscope can be considered as a series of Fourier transform from scattered waves from a specimen to a diffraction pattern and of inverse Fourier transform of the diffraction pattern to an image of the specimen. ψ(r) expresses scattered waves of the specimen, being the function of position r, and Ψ(k) expresses diffracted waves formed on the back focal plane of the imaging lens, being a function of the wave number k [1/m]. Φ(x)∝ψ(x/M) expresses the scattered waves on the imaging plane, which is an image of the specimen, being the function of position r. It is noted that Φ(x) is equal to ψ(r) shown in the second equation, except for a magnification M and image inversion caused by the lens.

Fig. 2 (a) Diffraction pattern (Fourier transform pattern) of an Au crystal. (b) Crystal lattice image of the Au crystal and its FFT pattern. Accelerating voltage: 300 kV.

Periodicities of the crystal lattice appear as bright diffraction spots on the back focal plane of the lens depending on the spacing and orientation of the lattice, by Fourier transform (a). A magnified image of the crystal lattice is obtained from the diffraction spots by inverse Fourier transform (imaging process of the lens) (b).

Related Term(s)