volume plasmon
volume plasmon
Collective oscillations of free electrons with a longitudinal wave or compressional-wave, which are induced in metals by an electron beam or a charged-particle, are called "volume plasmon". The volume plasmon is excited also in semiconductors and insulators. Its oscillation energy (plasmon energy) is proportional to the square root of the free electron density (valence electron density for semiconductors and insulators). The volume plasmon is directly observed as a peak in an electron energy-loss spectrum. It should be noted that the volume plasmon cannot be excited nor can be observed with a light wave or a transverse wave.
When a high-speed electron beam is incident on a solid metal, the Coulomb force formed by the beam induces a density change (compression) in the homogeneously distributed free electrons in the metal. With the induced Coulomb force as a driving force, a longitudinal oscillation wave of the free electrons with a specific frequency is created (see Fig.1). Quantization of this collective motion of the free electrons is called volume plasmon. The energy of the volume plasmon, EP, is expressed by the following equation.
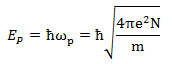
Here, ωp is the angular frequency of the plasma oscillation. ħ= h/2π is Planck’s constant. e, m, and N respectively express the elementary charge of an electron, the mass of an electron, and the density of the free electrons. The plasmon energy is proportional to the square root of the free electron density in a metal.
Although the volume plasmon is originally considered for free electrons, it is excited also in semiconductors and insulators as a collective oscillation of the whole valence electrons. The valence electrons vibrate collectively against positive ion cores. The energy or frequency of the plasmon is calculated by substituting the density of the valence electrons into the above equation.
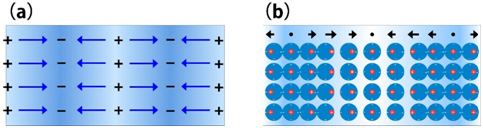
Fig. 1(a) Scematic of plasmon induced by free electrons. Metal is electrically nutral because free electrons and positive ions consisting of an atomic nuclei and inner shell electrons are homogenously distributed. When a high energy electron beam is incident on a metal from outside, the Coulomb force of the incident beam creates a density change in the free electrons, or positive and negative charged regions (indicated by (+) and (−) in Fig. 1(a)). With the electric field (indicated by blue arrows) caused by the density change as a driving force, the free electrons collectively starts a characteristic oscillation (plasma oscillation). (b) Schematic of plasmons of bounded electrons. Red dots and blue circles respectively show positive ions and valence electrons. The bounded valence electrons are displaced by the Coulomb force of the incident electron beam, density changes of the valence electrons being created. Then, the valence electrons collectively oscillate with plasma frequency. Black arrows at the top of Fig. 1(b) represent polarization caused by the displacements of the valence electrons. Plasma vibration of the bounded electrons is a longitudinal wave vibration caused by polarization of the atoms.
The charge density of Al is N = 1.8 × 1023 e/cm3. The plasmon energy is calculated to be 15.7 eV, showing a good agreement with an experimental value of 15.0 eV. For monovalent metals (Li, Na, etc.), the calculated energies agree well with the energies experimentally obtained.
For diamond (insulator), the plasmon energy is calculated to be 31 eV using the valence electron density (N = 7.0 × 1023 e/cm3), showing a rather good agreement with an experimental energy of 34 eV. In the cases of ionic crystals such as LiF, NaCl etc., their plasmon energies calculated using the valence electron densities well reproduce the energies experimentally obtained. Table 1 shows the plasmon energies for various materials.
However, for a material in which interband transitions strongly occur close to the expected plasmon energy, the experimental plasmon energy can be largely deviated from the expected energy. For example, in the case of Ag, the plasmon energy expected from the valence electron density of N=0.59×1023 e/cm3 is 9.0 eV but the experimental plasmon energy is observed at 3.9 eV due to a strong interband transition of the d orbital electrons at 4.0 eV.
Table1. Plasmon energies for several materials
| Materials | Valence electron density [e/cm3] | Ep [eV] (Calculation) | Ep [eV] (Experiment) |
|---|---|---|---|
| Li | 0.47 × 1023 | 8.0 | 7.1 [1] |
| Na | 0.27 × 1023 | 6.1 | 5.7 [1] |
| Al | 1.8 × 1023 | 15.7 | 15.0 |
| Ag | 0.59 × 1023 | 9.0 | 3.9 |
| Si | 2.0 × 1023 | 16.5 | 16.7 |
| GaAs | 1.8 × 1023 | 15.7 | 15.9 |
| Diamond | 7.0 × 1023 | 31 | 34 |
| LiF | 4.9 × 1023 | 25.9 | 25.3 [1] |
| NaCl | 1.8 × 1023 | 15.7 | 15.5 [1] |
[1] H. Raether (1980) "Excitation of Plasmons and Interband Transitions by Electrons" Springer Tracts in Modern Physics, Vol. 88, Springer-Verlag. New York.
(By Associate Professor Yohei Sato, Tohoku University)
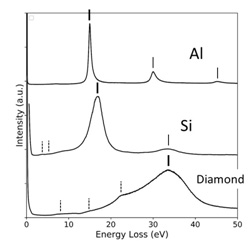
Fig. 2. Plasmon peaks of Al, Si and Diamond in EELS spectra
Related Term(s)
Term(s) with "volume plasmon" in the description
Are you a medical professional or personnel engaged in medical care?
No
Please be reminded that these pages are not intended to provide the general public with information about the products.




