extinction distance

The extinction distance is the distance of a period over which the intensity of electrons incident on a crystalline specimen repeat decrease and increase with the penetration depth.

Consider the case where an electron wave incident on a crystalline specimen causes a single Bragg reflection (called “two-wave approximation”). The incident (transmitted) wave is reflected by a set of crystal lattice planes and damps with the depth of the specimen. The reflected wave increases with the depth. When a certain depth t is reached, the amplitude of the transmitted wave becomes zero and the amplitude of the reflected wave becomes maximum.
As the depth increases further, the reflected wave is reflected toward the transmitted wave. When the depth reaches 2t, the amplitude of the reflected wave becomes zero again and the amplitude of the transmitted wave becomes maximum. In such a manner, the amplitudes of the transmitted and reflected waves alternately decrease and increase with the depth (called “Poendel Loesung” solution in dynamical electron diffraction). The repetition period 2t is termed “extinction distance” ξ_ｇ.

The extinction distance is expressed by ξ_ｇ= $\frac{\mathrm{\pi V<span\; class="m-sub">c</span>}}{\mathrm{\lambda <i>F</i><span\; class="m-sub"><font\; face="ＭＳ\; Ｐ明朝,ＭＳ\; 明朝">ｇ</font></span>}}$. Here, V_c is the unit cell volume of a crystal, λ is the wavelength of an incident electron, and Ｆ_ｇ is the crystal structure factor of reflectionｇ. Since the crystal structure factor Ｆ_ｇ corresponds to the reflectivity of reflection g, for a reflection with a larger Ｆ_ｇ the transmitted wave is transferred faster to the reflected wave, and then the extinction distance becomes shorter. That is, ξ_ｇ is inversely proportional to Ｆ_ｇ. When the accelerating voltage of the incident electron increases, the interaction between the incident wave and the crystal (or the reflectivity of the crystal) decreases. The extinction distance becomes longer at a higher accelerating voltage or at a shorter wavelength. Thus, the extinction distance ξ_ｇ is inversely proportional to the wavelength of the incident electron. The wavelength of the electron is inversely proportional to the one-half power of the accelerating voltage.

Fig. 1 illustrates schematically how the transmitted and reflected waves alternate in intensity with the depth of the specimen.

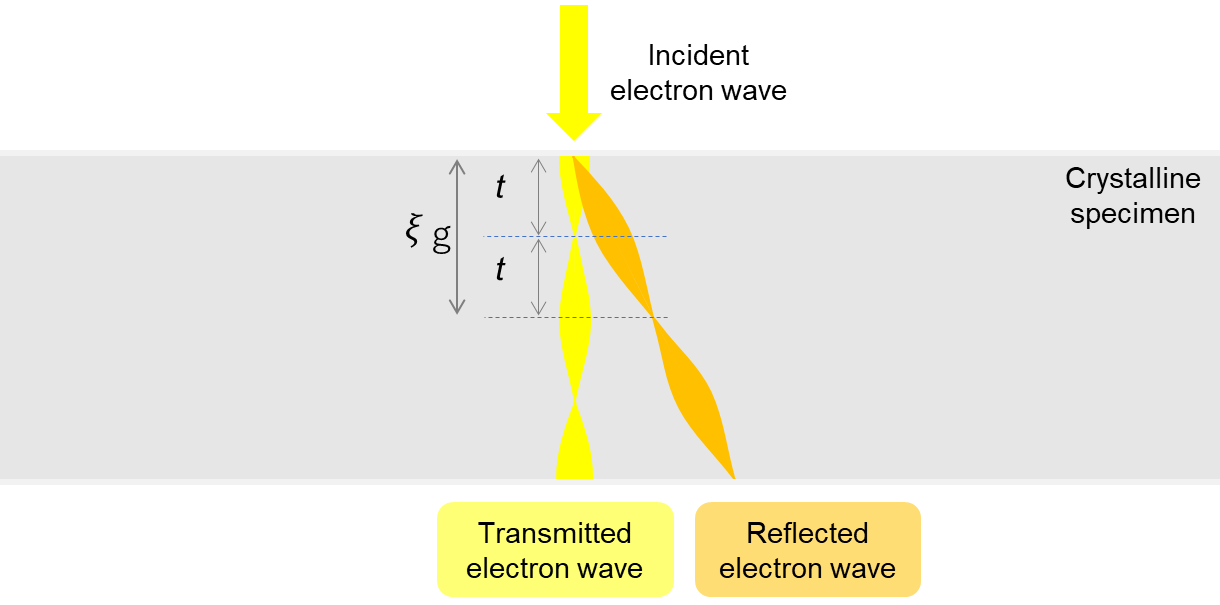
Fig. 1. Schematic of the intensity change of the transmitted and reflected waves in a specimen. The intensities of the transmitted and reflected waves alternately decrease and increase with the depth of the specimen (the repetition period being the extinction distance ξ_ｇ).

Table below lists the reflection dependence and the accelerating voltage dependence of the extinction distances for Al, Si, Cu and Au. Since the value of the crystal structure factor Ｆ_ｇ is larger for lower-order reflections, and is larger for a larger atomic number Z, the corresponding ξ_ｇ becomes shorter. It is also seen that as the wavelength becomes shorter with the increase of the accelerating voltage, ξ_ｇ becomes longer.
In experiments, the extinction distance is observed as the equal thickness fringes when using a wedge-shaped crystal.

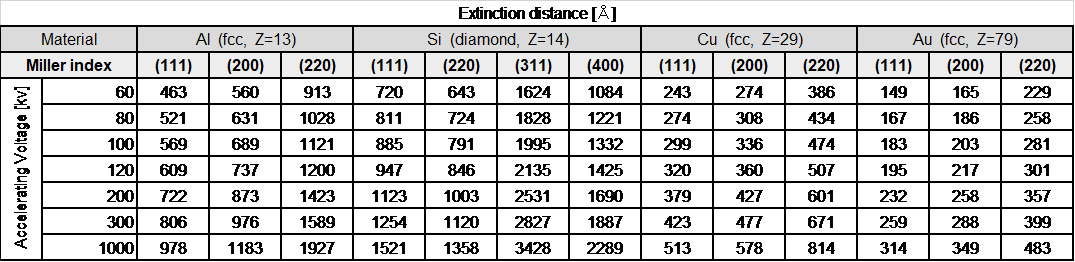
Table: Extinction distances for Al, Si, Cu and Au.
(reprinted from M. Tanaka, M. Terauchi, K. Tsuda, “Introduction to Electron Diffraction and Elementary Crystallography (in Japanese)”, Kyoritsu Printing Co., Ltd., 2014)

Related Term(s)