crystal structure factor

The crystal structure factor represents the amplitude and phase of a diffracted wave (reflected wave)from a unit cell of a crystal. The factor is given by the atom species and their positions in the unit cell. From the crystal structure factor, the relative intensity of the reflected wave and the extinction rule of the reflections are obtained.The crystal structure factor F_gis expressed as the next equation.

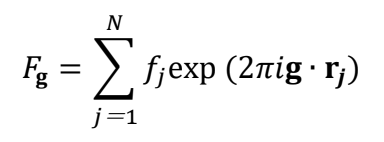
Here, f_j is the atomic scattering factor of thej-th atom in a unit cell, g is the reciprocal lattice vector, and r_j is the coordinate of the j -th atom. The summation is performed over all the atoms in the unit cell. The phase term exp represents a difference in the phase of the wave from each atom when a diffracted wave changes the direction by the reciprocal lattice vector g with respect to the incident wave. Fig. 1 shows the relation between the incident wave k₀, the diffracted wave k and the reciprocal lattice vector g.

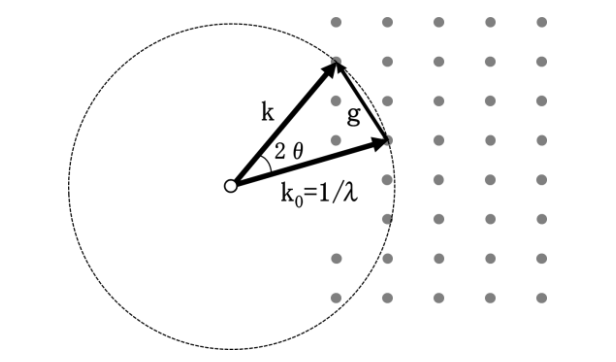
Fig. 1. Relation between the incident wave k₀, the diffracted wave k and the reciprocal lattice vector g. The magnitude of k₀ is 1/λ (λ: wavelength). The incident wave causes a certain reflection g by crystal, then the diffracted wave (reflection beam) travels in the direction of k (= k₀+ g). It is noted that in the figure, k is depicted in a short length for convenience: for an incident electron beam of 200 kV, the magnitude of k₀ is more than 50 times larger that of the reciprocal lattice vector g.

g can be written as g=ha^*+kb^*+lc^* using the reciprocal lattice vectors and three indices of the reflection. r_j can be written as r_j = u_ja + v_jb + w_jc using the unit cell vectors and the components of positional coordinates of the atoms. Substituting these into the above equation F_g,

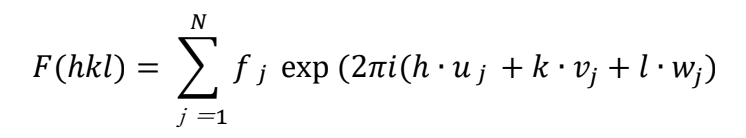
Here, |F(hkl )|² expresses the relative intensity of the hkl reflection. If F(hkl )=0, the reflection hkl disappears.

As an example, the reflection intensity and extinction rule for the body-centered cubic structure are given. In the body-centered cubic structure, the atomic positions in the unit cell are 000 and 12 12 12.
Then, the following results are obtained.

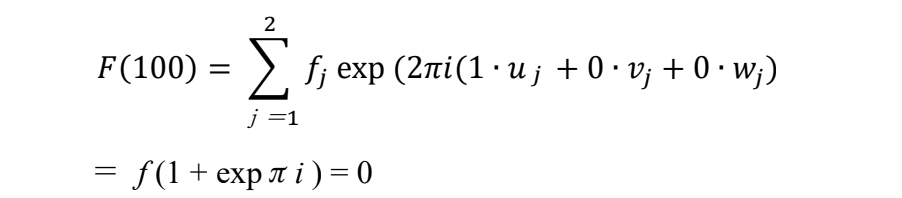
That is, the 100 reflection disappears.

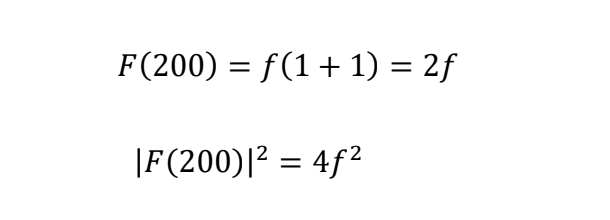
Thus, the intensity of the 200 reflection is proportional to 4f ². When the sum of the indices h + k + l is an even number, the diffracted wave has intensity, but when the sum is an odd number, the diffracted wave disappears (extinction rule).

Related Term(s)