Green's function

The Green's function G(x,x') is a function that gives the effect (response and propagation) of a point scatterer at x' on a point x. In the following, two mathematical models are used as examples to explain how the Green's function is used to solve the problems.

Example 1. Consider the equation Δφ=-ρ/ε₀ (Poisson's equation), which is satisfied by the potential φ produced by the charge distribution ρ. If the inverse of the differential operator such that Ĝ=Δ^-1 is obtained, the solution can be obtained as φ=-Ĝρ/ε₀. The integral operator Ĝ is called the Green operator, and the integral kernel G( x, x' ) ≔ ⟨ x│Ĝ│x' ⟩ expressed in real space is called the Green's function.

From the definition, Δ⋅Ĝ=1 (Identity transformation), the following equations are derived.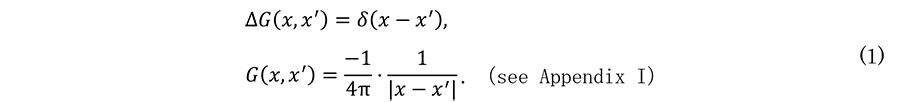

Then, the integral form solution of φ is obtained.

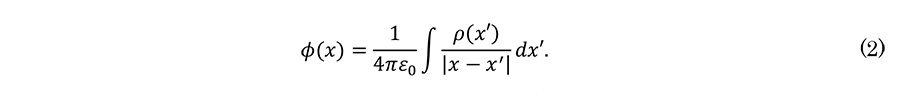
Here, G(x,x') can be regarded as a response function that gives the potential φ(x) formed at the point x by the charge ρ(x') at the point x’.

Example 2. In the dynamical theory of electron diffraction, an electron incident on a crystal follows the steady-state Schrodinger equation [Δ+K²]ψ=-Uψ, where K is the wave number vector of the incident electron and U(r) is the potential energy distribution of the crystal.
By letting Ĝ=[Δ+K² ]^-1, the solution can be obtained as ψ=-ĜUψ. From the definition, [Δ+K² ]⋅Ĝ=1 (Identity transformation), the following equations are derived.

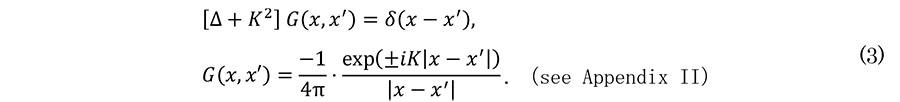
Then, the integral form solution of ψ is obtained.

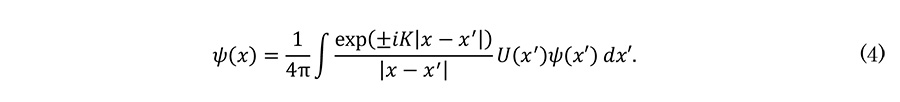
Here, G(x,x') can be regarded as a response function that gives the wave function ψ(x) formed at the point x by the wave function ψ(x') and the scatterer U(x') at the point x'. It can also be regarded as a propagator that gives the probability of the change of the electron wave from |x' ⟩ to that of |x ⟩ by the scatterer U.

Equation (4) is solved by an iterative approximation, since ψ is also included in the integral on the right-hand side.
In the scattering problem, the solution at infinity (particular solution for U=0) is the incident plane wave φ(x')=exp(iKx'). The first-order approximate solution is obtained by substituting the plane wave into the right-hand side of eq. (4) as ψ=φ-ĜUφ (Born approximation). This formulation corresponds to finding the scattered wave that is scattered only once, and the resulting scattering amplitude is proportional to the Fourier coefficient of U.

Appendix I. Proof of eq. (1).

Let V be a sphere with radius r centered on the origin, and S be its surface. Then, from Gauss's divergence theorem we obtain,

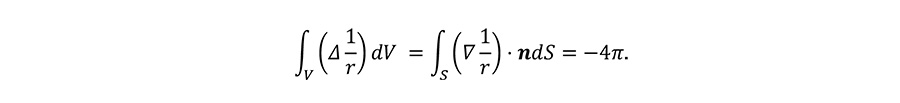
Since the integral does not depend on the radius r, the integrand is proved to be a delta function, i.e.,

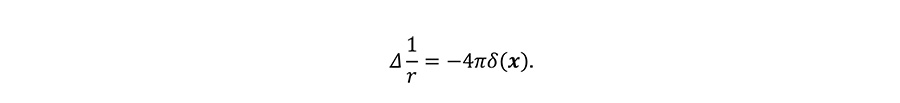
Appendix II. Proof of eq. (3).

From the analogy of eq. (1), the solution of eq. (3) is expected in a form of G(x,x')= f(r)/r, (r=|x-x'|). Substituting this, we obtain f''+K²f=0. By solving this equation, we obtain f(r)=C exp(±iKr).

Related Term(s)