reciprocal lattice

“Reciprocal lattice” is composed of the points (reciprocal lattice points) which are created in the directions perpendicular to the lattice planes at the distances reciprocal of the spacings of the (crystal) lattice planes in the real space. The reciprocal lattice is derived uniquely from the real lattice through a mathematical transformation.

The basis vectors a*, b* and c* of the reciprocal lattice are defined by the following equations using the basis vectors a, b and c of the real lattice.

Each denominator of these equations is equal to the volume V of the unit cell of the real lattice. That is,

V=a∙(b×c)=b∙(c×a)=c∙(a×b).(2)

Then, a*, b* and c* are written as

a* is vertical to the plane spanned by b and c of the real lattice. In the same manner, b* is vertical to the plane spanned by c and a, and c* is vertical to the plane spanned by a and b.

The reciprocal lattice is constructed by a linear combination of a*, b* and c*. The reciprocal lattice vector g is written with integers h,k,l as

g = ha*＋kb*＋lc*.(4)

The reciprocal lattice vector g is vertical to the crystal lattice plane (h k l) (termed “Miller index”) in the real space. The magnitude (length) of the vector g is reciprocal of the spacing d of the lattice plane (h k l), or｜g｜＝ 1/d. The dimensions of basis vectors of a*, b* and c* are [r]^-1, whereas the dimensions of basis vectors of a, b and c are [r]¹. So, the lattice constructed by a*, b* and c* is called “reciprocal lattice”.

The advantage of using the reciprocal lattice is that a crystal lattice plane can be treated as a reciprocal lattice point, that is “planes” are expressed as “points”. When the Ewald construction in the reciprocal lattice space is used, it is easy to find which lattice planes satisfy the reflection condition (Bragg condition). Drawing of the Ewald’s diagram is carried out in the following manner.

The dots in the figure show the reciprocal lattice points. Select one of the reciprocal lattice points and set the origin at a point that is 1/λ(=|k₀|) distant from that point in the direction anti-parallel to the direction of the incident electron beam. Draw an arrow line from the origin to the chosen reciprocal lattice point. The arrow line is the vector k₀ of the incident electron beam. Then, draw a sphere of radius 1/λ centered on the origin (Note that the figure shows not a sphere but a two-dimensional circle). This is called the Ewald sphere. All of the reciprocal lattice points intersecting the Ewald sphere satisfy the Bragg condition. A vector ｋ from the origin to a reciprocal lattice point g is the vector of the reflected beam. From the figure, the following equation is derived as the reflection condition.

ｋ-ｋ₀ = g.(5)

This is named the Laue condition. The incident beam withｋ₀ is reflected by a lattice plane (h k l) of a crystal and changes its direction by g toｋ=ｋ₀＋g, and is outgoing from the crystal in the directionｋ.

Letting the angle between ｋ₀ and ｋ be 2θ, the magnitude of ｋ-ｋ₀ becomes ( $\frac{1}{\lambda }$ )×2sinθ. Since the magnitude of g is 1/d, the following equation is obtained from eq.(5).

This equation is rewritten as

2dsinθ=λ.(7)

Equation (7) is the Bragg equation. Therefore, it becomes clear that the Laue condition derived from the Ewald’s diagram is equivalent to the Bragg condition.

The Bragg condition expresses diffraction by a crystal using a scalar quantity in the real space. Thus, the Bragg condition is intuitive and easy to understand. On the other hand, the Laue condition expresses diffraction using a vector quantity in the reciprocal space. Thus, the Laue condition is abstract but is suitable for theoretical treatment of diffraction phenomena. The use of the Laue condition is crucial for advanced theory of diffraction.

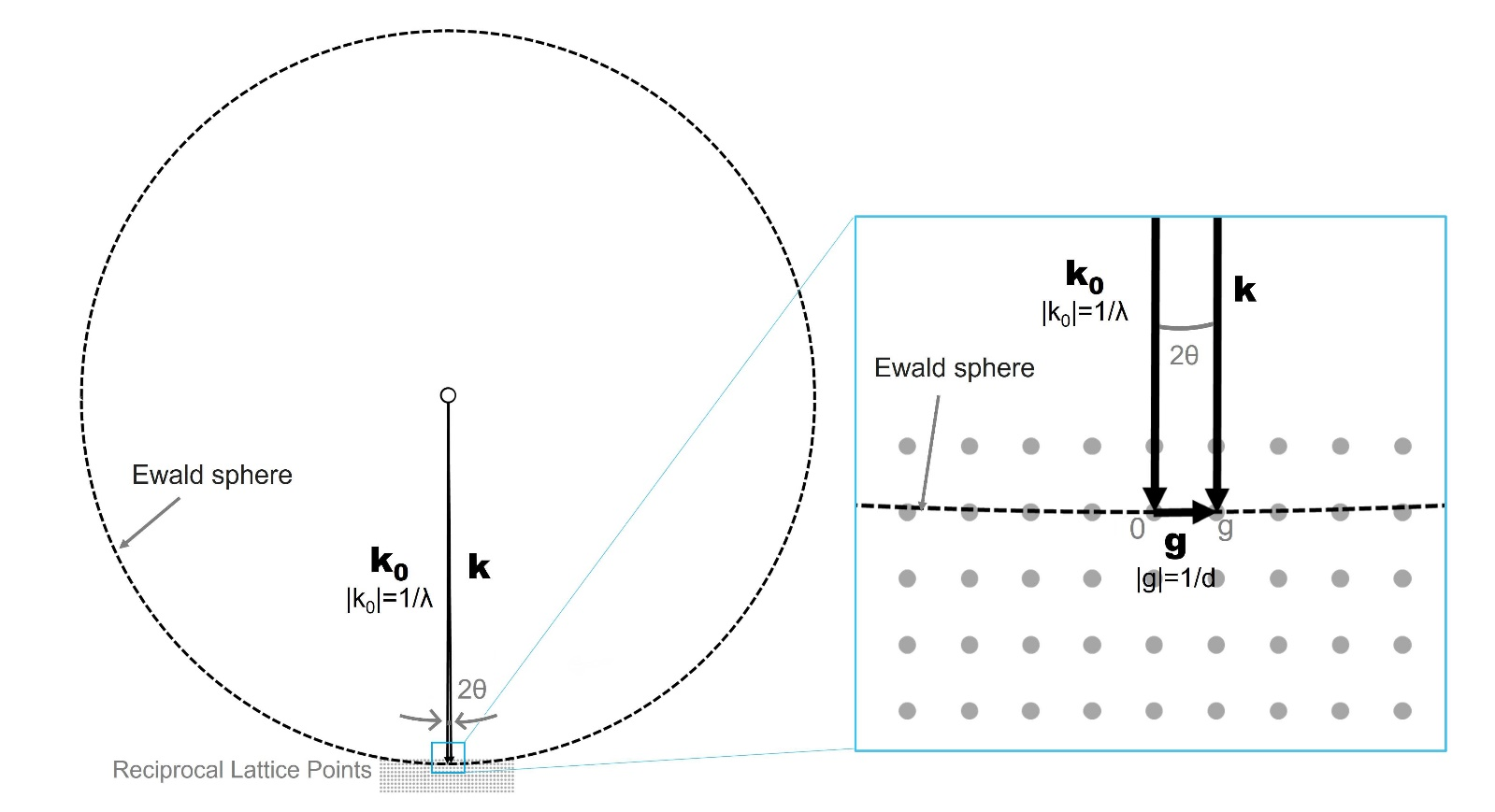
Fig. Reciprocal lattice and Ewald sphere. An enlarged figure of the bottom part in the left diagram is shown on the right to see the relation between the reciprocal lattice vector g and the incident wave vector k₀ & the reflection wave vector k.
In the case of the electron microscopy, the radius of the Ewald sphere is 27.0 [Å^-1] even at an acceleration voltage of 100 kV. The spacing of the reciprocal lattice points is ~0.5 [Å^-1]. Then, the radius of the sphere is very large, more than 50 times larger than the spacing of the reciprocal lattice points. The Ewald sphere is regarded approximately as a flat plane. Thus, the Ewald sphere nearly intersects many reciprocal lattice points and many reflections appear simultaneously in the electron diffraction pattern.

Related Term(s)