Phi-Rho-Z method (φ(ρz) method), PRZ
Phi-Rho-Z method (φ(ρz) method)
The Phi-Rho-Z method (φ(ρz) method) is one of quantitative correction methods in obtaining the mass concentrations of the constituent elements of a specimen using characteristic X-rays generated by an electron beam.
The method uses the depth distribution of the generated characteristic X-rays, where the atomic number (Z) effect and the absorption (A) effect are simultaneously taken into account. Then, the φ(ρz) method provides a higher accuracy quantitative correction than the ZAF correction method in which the both effects are separately treated. In particular, the φ(ρz) method can provide more accurate results than ZAF correction especially in the cases requiring accurate absorption correction; for the specimens consisting of light elements and heavy elements, and for the high accelerating voltages of the incident electron beam where the characteristic X-rays are generated over a deep region in the specimen. The depth distribution of the characteristic X-rays is given by a functionφ(ρz), where ρ is the mass density, z is the depth from the specimen surface and then ρz expresses the mass depth.
Consider a bulk specimen to be composed of stacking of thin layers with each thickness Δ(ρz). The intensity of the characteristic X-rays ΔI(ρz) generated from a layer at a certain mass depth ρz (left figure in Fig. 1) is different from the intensity of the characteristic X-rays ΔI generated from a single thin film with the same mass thickness (right figure in Fig. 1), and needs to multiply the generation function φ(ρz) to the intensity ΔI because the electron beam is scattered before reaching the layer at the mass depth ρz.
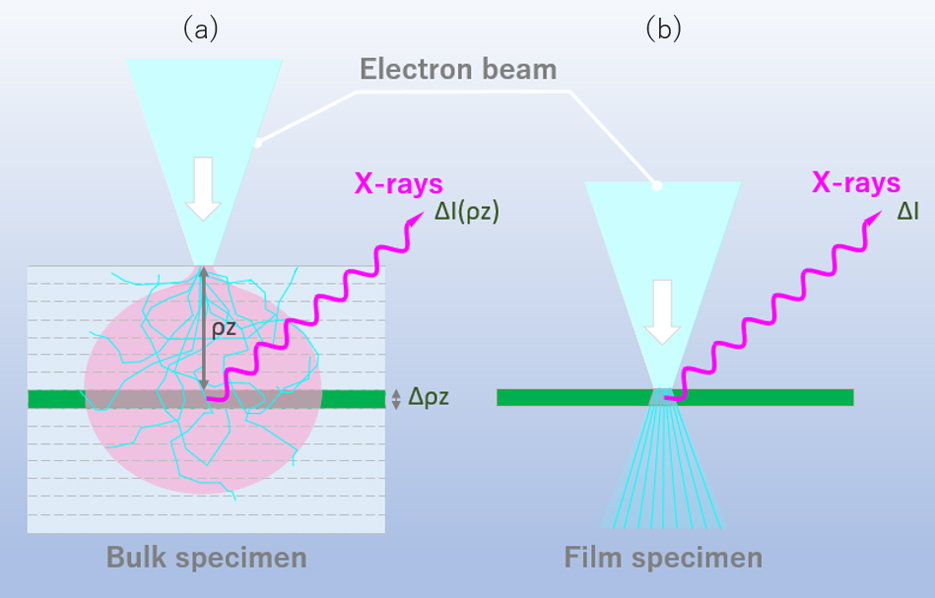
Fig. 1 Difference of the intensities of the generated characteristic X-rays between a bulk specimen (a) and a single thin-film specimen (b). In a bulk specimen, the incident electron beam is scattered until the beam reaches the layer at the mass depth ρz. Thus, the intensity of the characteristic X-rays ΔI(ρz) generated at depth Δ(ρz) needs to multiply the generation function φ(ρz) to the intensity of the characteristic X-rays ΔI from a single thin-film specimen.
Some model functions for φ(ρz) have been proposed. They have such ρz dependence as shown in Fig. 2. That is, the value of φ(ρz) increases up to the mass depth (ρz m) due to the fact that an electron beam changes their travelling direction by scattering and the flight distance in each layer becomes longer to increase the exciting probability of the characteristic X-rays. Also, backscattering from a deeper region of the specimen contributes to increase the X-ray generation. The value ofφ (ρz) decreases when the depth is greater than ρz m because, by scattering, the number of the penetrating electrons decreases and the penetrating electron energies become small to excite the characteristic X-rays.
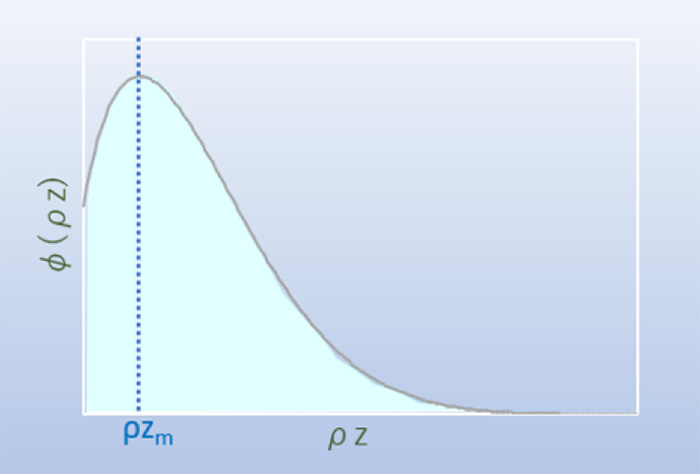
Fig. 2 Generation function φ(ρz)
Dependence of the characteristic X-ray generation function φ(ρz) on the mass depth (ρz). The function increases up to a certain mass depth ρz m, and decreases beyond the depth.
The intensity of the characteristic X-raysΔIA(ρz) from element A generated at a certain mass depth ρz is expressed by the following equation,
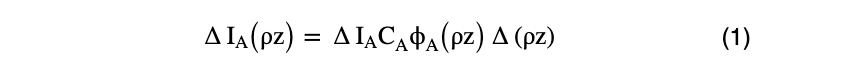
Here, ΔIA is the intensity of the characteristic X-rays of element A emitted from the thin-film specimen with mass thickness Δ(ρz), CA is the mass concentration [mass%] of element A, φA(ρz) is the generation function for element A, ρ is the mass density of the specimen, and z is the depth of the specimen.
The intensity of the characteristic X-rays ΔIA(ρz) suffers absorption which depends on the path length of the characteristic X-rays in the specimen until those X-rays are emitted out of the specimen (Fig. 3). The magnitude of absorption depends on the mass absorption coefficient of the specimen and on the path length of the X-rays travelling toward the X-ray detector, and is expressed by an attenuated exponential function. Thus, the intensity of the characteristic X-rays ΔI’A(ρz) measured by the X-ray detector (placed outside the specimen) is expressed as
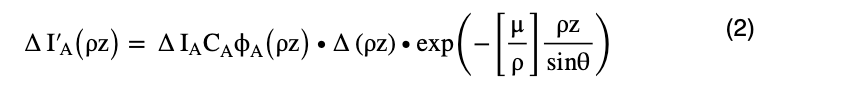
Here, [μ/ρ] is the mass absorption coefficient for the characteristic X-rays of element A in the specimen, and θ is the take-off angle of the X-ray detector against the specimen surface.
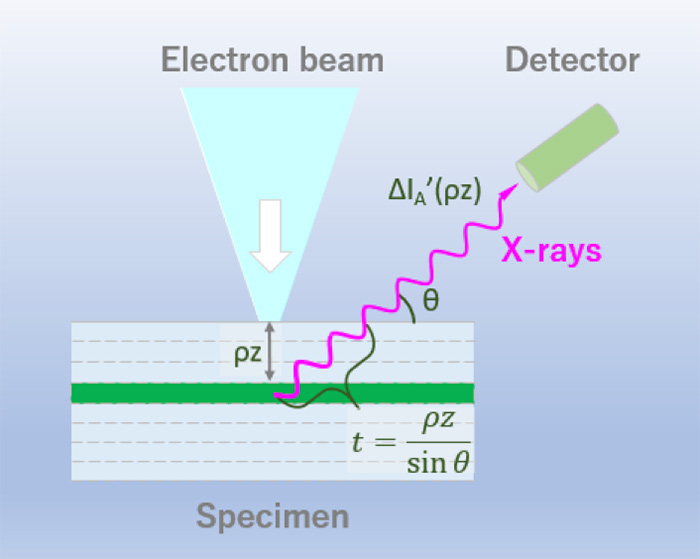
Fig. 3 Path length of the characteristic X-rays in the specimen toward the X-ray detector. The path length is expressed as t = ρz/sinθ, where ρz is the mass depth and θ is the take-off angle of the X-ray detector against the specimen surface.
The intensity of the characteristic X-rays ΔI’A detected is obtained by integrating the equation (2) with respect to the mass depth ρz, and expressed as
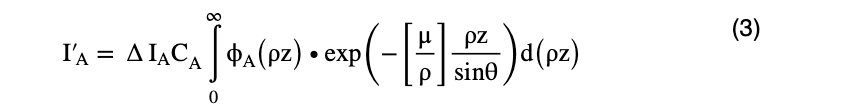
Thus, the detected characteristic X-ray intensity ratio of the unknown specimen to that of the standard specimen (chemical composition is known) is expressed by the following equation.
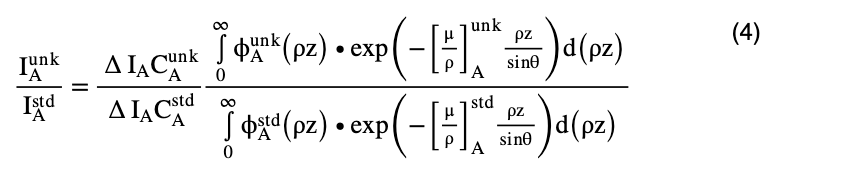
Here, 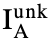 is the characteristic X-ray intensity of element A detected from the unknown specimen, and
is the characteristic X-ray intensity of element A detected from the unknown specimen, and  is the characteristic X-ray intensity of element A detected from the standard specimen.
is the characteristic X-ray intensity of element A detected from the standard specimen. 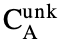 is the mass concentration of element A in the unknown specimen, and
is the mass concentration of element A in the unknown specimen, and 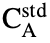 is the mass concentration of element A in the standard specimen.
is the mass concentration of element A in the standard specimen. 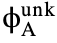 (ρz) is the generation function of element A in the unknown specimen, and
(ρz) is the generation function of element A in the unknown specimen, and 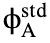 (ρz) is the generation function of element A in the standard specimen.
(ρz) is the generation function of element A in the standard specimen. 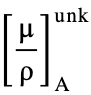 is the mass absorption coefficient for the characteristic X-ray of element A in the unknown specimen, and
is the mass absorption coefficient for the characteristic X-ray of element A in the unknown specimen, and 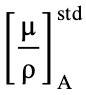 is the mass absorption coefficient for the characteristic X-ray of element A in the standard specimen.
is the mass absorption coefficient for the characteristic X-ray of element A in the standard specimen.
Then,
Using the equation 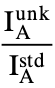 = K (K ratio), the equation (4) is rewritten as
= K (K ratio), the equation (4) is rewritten as
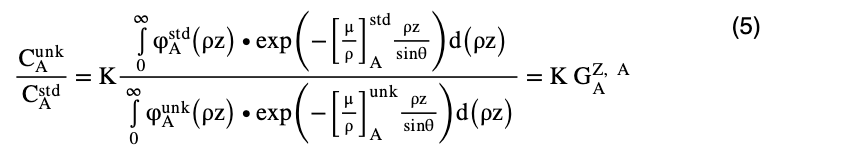
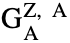 is the correction factor for the atomic number effect and the absorption effect in the φ(ρz) method. In addition, like the case of ZAF correction, by taking into account the fluorescence correction factor (
is the correction factor for the atomic number effect and the absorption effect in the φ(ρz) method. In addition, like the case of ZAF correction, by taking into account the fluorescence correction factor (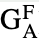 ), the quantitative correction factor (G) in the φ(ρz) method finally becomes
), the quantitative correction factor (G) in the φ(ρz) method finally becomes
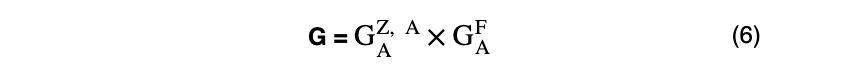
Reference:
Joseph I. Goldstein, Dale E. Newbury, Joseph R. Michael, Nicholas W.M. Ritchie, John Henry J. Scott and David C. Joy (2017) “Scanning Electron Microscopy and X-ray Microanalysis 4th edition” springer.
Related Term(s)
Term(s) with "Phi-Rho-Z method (φ(ρz) method)" in the description
Are you a medical professional or personnel engaged in medical care?
No
Please be reminded that these pages are not intended to provide the general public with information about the products.




