Double Stimulated Echo (DSTE) Experiments for Thermal Convection Compensation in PFG-NMR
NM220005
Pulsed-Field Gradient NMR (PFG-NMR) is utilized for analyzing the self-diffusion of molecules and ions, which are commonly referred to as 'particles' in this context. The translation of particles by thermal convection significantly impacts the decay curve in PFG-NMR experiments, particularly when dealing with solution and liquid samples. In cases where the convection-induced translation is substantial, the decay curve exhibits a cosine-like behavior, leading to an apparent increase in the self-diffusion coefficient compared to the actual value. Additionally, the decay curves may become distorted, occasionally resulting in the appearance of signals in negative phase. To address this convection artifact in PFG-NMR, Double Stimulated Echo (DSTE) experiments [1] are specifically designed and employed.
PFG-NMR
PFG-NMR is a technique used to analyze the self-diffusion of particles. The self-diffusion of particles arises from random Brownian motion, where the displacement at a given time follows a Gaussian probability distribution. In PFG-NMR, the displacement along the z-axis is encoded using pulsed-field gradients in the z-direction. Here, the probability distribution (P(Δz, t)) of the displacement (Δz) along the z-axis within a given time (t) is represented by formula 1, where D is the self-diffusion coefficient.
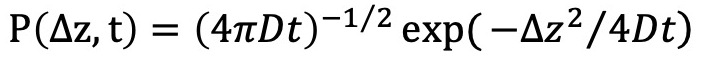 (1)
(1)
Figure 1 shows the Pulsed Gradient Spin Echo (PGSE) sequence, which is the simplest PFG-NMR experiment. Here, a spin-echo experiment is conducted with two gradients of equal strength applied before and after the refocusing pulse. The two gradients operate in opposite directions with respect to the refocusing pulse. If the particle remains stationary during the experiment, the first gradient dephases the magnetization, and then the second gradient rephases the magnetization. Consequently, the signal intensity remains unmodulated (when neglecting relaxation and J-coupling evolution in this context). However, the displacement along the z-axis during the experiment, particularly during the period between the two gradients known as the diffusion time (D), leads to phase modulation caused by incomplete re-phasing (as described by formula 2).
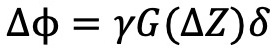 (2)
(2)
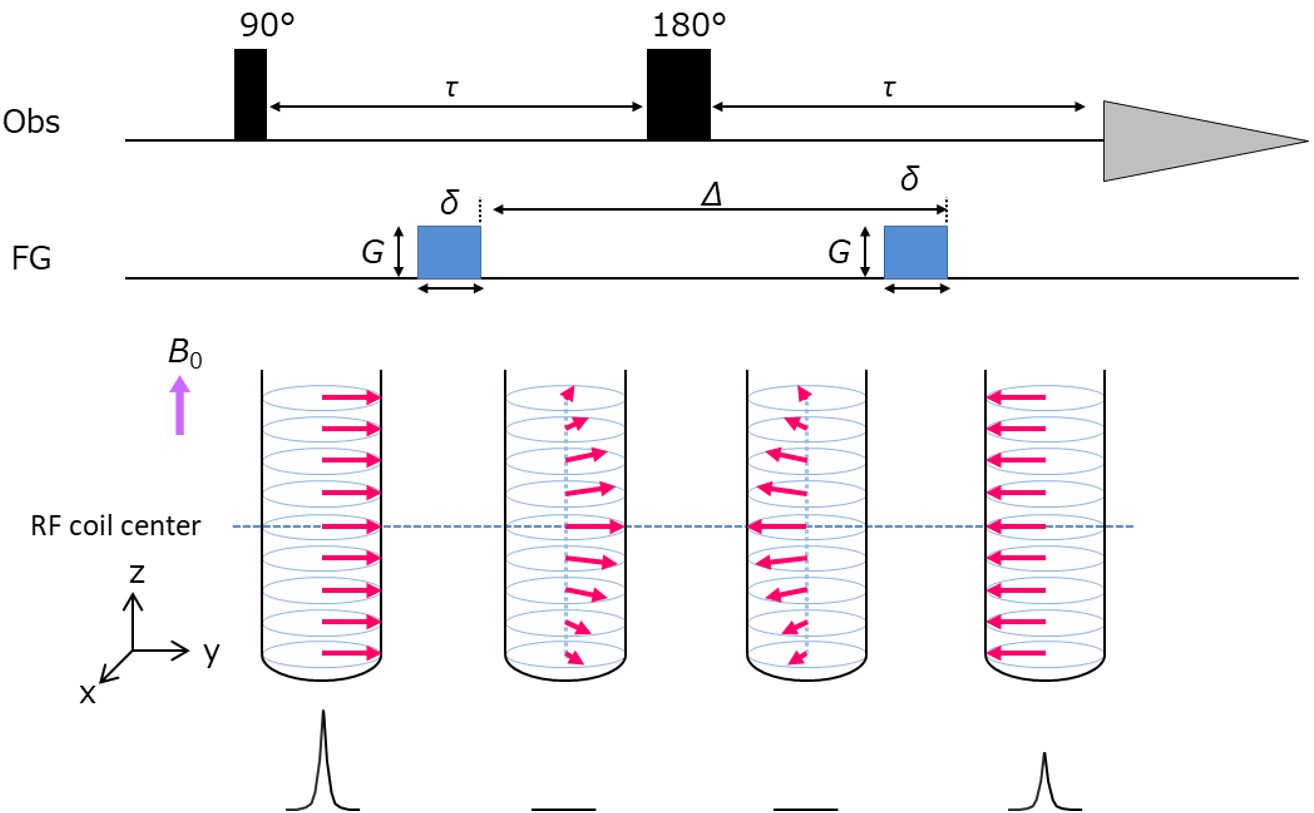
Figure 1 The pulse sequence of the PGSE experiment and the encoding of z-axis displacement through the gradient applied along the z-axis.
Here, the probability distribution of the modulated phase is given by formula 3, which combines the z-axis distribution described in formula 1 and the phase modulation outlined in formula 2. In this context, the gyromagnetic ratio is represented by γ, the gradient strength of gradient is denoted as G, the duration of gradient is indicated as δ, and the diffusion time is represented as Δ.
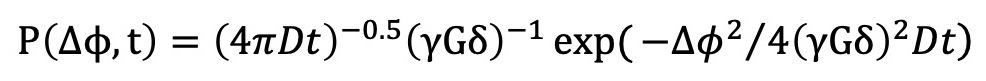 (3)
(3)
An important aspect highlighted in this note is that the average of the phase modulation (PΔφ, t) is 0. Additionally, the signal intensity is reduced as the phase distribution becomes more spread out, as described by formula 4, commonly known as the Stejskal-Tanner formula [2].
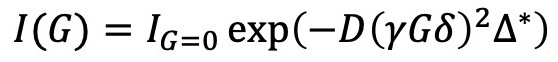 (4)
(4)
Here, IG=0 represents the signal intensity at G=0, and Δ* corresponds to the correlated diffusion time, accounting for the gradient's shape factor [3]. I(G) exhibits a (half) Gaussian distribution with respect to G and an exponential decay with respect to G2. The self-diffusion coefficient (D) is obtained by recording the decay of signal intensity through a series of PFG-NMR experiments conducted with varying gradient strengths. The obtained data is then fitted using either the Stejskal-Tanner formula or inverse Laplace transform for accurate determination of D.
Thermal convection in PFG-NMR
The temperature gradient within a solution in an NMR tube can induce thermal convection. Formula 5 represents Rayleigh-Bénard convection in a long cylindrical sample, such as a solution inside an NMR tube [4].
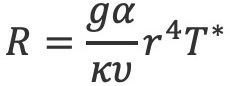 (5)
(5)
In this context, g represents the gravitational acceleration, α stands for thermal expansivity, κ denotes thermal diffusivity, υ represents kinetic viscosity, r signifies the inner diameter of the NMR tube, and T* represents the temperature gradient along the length of the sample. When the Rayleigh number exceeds the critical number, heat transport is driven by both convection and thermal conduction. Several practical approaches have been proposed to mitigate thermal convection. These include reducing the sample height (thus decreasing T*) by using microtubes or similar methods, employing high-viscosity solvents (increasing υ), and using NMR tubes with smaller inner diameters than usual (reducing r ), such as 3 mm NMR tubes.
Here, we make the simplifying assumption that the translation velocity due to thermal convection remains constant (v) for the purpose of simulation. Although the average of phase modulation is 0 in the absence of convection, it is shifted by the translation caused by thermal convection during the diffusion time. As a result, a cosine-like behavior is observed in the signal decay of PFG-NMR experiments, as described in reference [5] and formula 6.
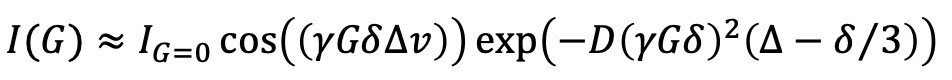 (6)
(6)
Double Stimulated Echo (DSTE)
The DSTE experiments are specifically designed to mitigate the undesired signal intensity modulation caused by convection in PFG-NMR [1]. The fundamental concept behind DSTE is to utilize two echoes with gradients, orienting them in opposite directions, in order to counteract phase modulation caused by convection velocity. Practically, the pulse sequence depicted in Figure 2(a) utilizes two gradient echoes with the following polarities of gradient pulses: +,- and -,+ within a single pulse experiment. The first gradient echo and the second gradient echo are oriented in opposite directions, effectively canceling out the phase modulation caused by convection velocity. PFG-NMR experiments with convection compensation can be achieved by combining z-axis displacement encoding with the scheme illustrated in Figure 2(a).
Pulsed Gradient Stimulated Echo (PGSTE), an advanced version of PGSE, is utilized in DSTE experiments. The PGSTE block positions the magnetization along the z-axis, enabling robustness against fast transverse relaxation and homonuclear J-coupling modulation. The DSTE pulse sequence depicted in Figure 2(b), as indicated by its name, incorporates two PGSTE units within the sequence. The coherence order of the four gradients in PGSTE is designed as p=-1, +1, +1, -1 in the solid line using phase cycling. This arrangement ensures that the two STEs work in opposite directions to compensate for phase modulation caused by convection velocity. The corresponding pulse program in the Delta NMR software version 6 for this DSTE experiment is named 'dste_led_diffusion.jxp'. Figure 2(c) presents a bipolar pulse pair (BPP) version of the DSTE experiment, which is also available. In the Delta NMR software version 6, the corresponding pulse program is named 'bpp_dste_led_diffusion.jxp', while in Delta V5, it is referred to as 'bpp_dste_led_dosy_pfg.jxp'.
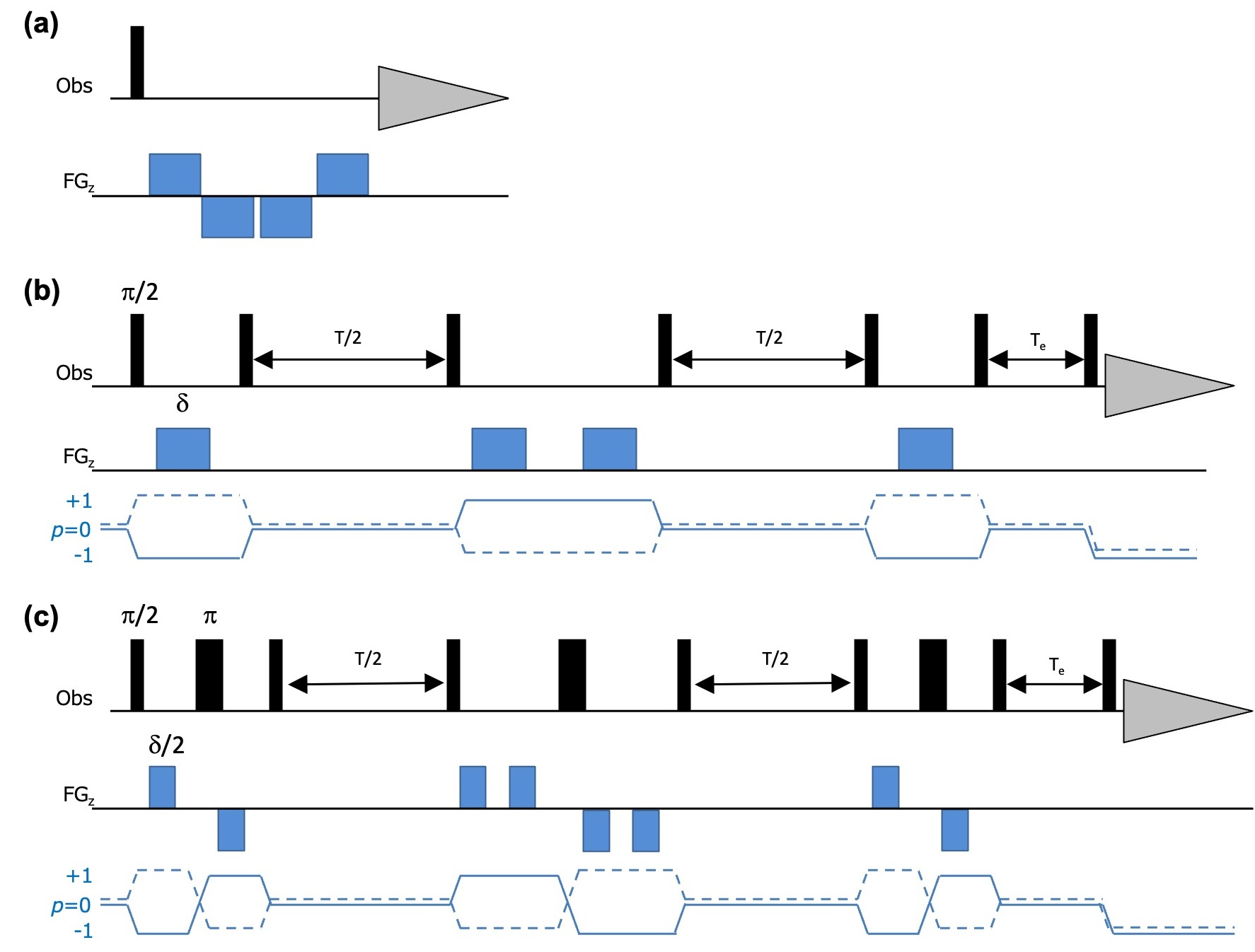
Figure 2 Compensating thermal convection by double echo: (a) double gradient echo, (b) DSTE: Delta V6 - dste_led_diffusion.jxp, (c) BPP-DSTE: Delta V6 - bpp_dste_led_diffusion.jxp, Delta V5 - bpp_dste_led_dosy_pfg.jxp. 'p' represents the selected coherence order.
Comparing practical applications of DSTE and PGSTE techniques
Figure 3 illustrates practical comparisons of DSTE and PGSTE, demonstrating the presence of thermal convection artifact in PGSTE and its compensation in DSTE. PGSTE and DSTE experiments were conducted under identical acquisition parameters (Δ=200 ms, δ=5 ms, G=30-270 mT/m) at 90 degrees Celsius, using a 4 w/v% polystyrene (31 kDa, for GPC) solution in o-dichlorobenzene-d4. The signal decay in the PGSTE spectrum, as shown in Figure 3(a), is faster compared to the DSTE spectrum depicted in Figure 3(b). The intensities of the signal corresponding to the polystyrene aromatic proton at 6.96 ppm are presented in a Stejskal-Tanner plot shown in Figure 3(c). In the PGSTE data, the initial decay is utilized for the plot, even though the non-initial decay does not adhere to the Stejskal-Tanner formula. The negative slope observed in the plot corresponds to the self-diffusion coefficient. The 'apparent' self-diffusion coefficients obtained from the PGSTE experiments were larger than the actual diffusion coefficient determined in DSTE. Furthermore, it was observed that the 'apparent' self-diffusion coefficients were proportional to the diffusion time employed in the STE experiments, as depicted in Figure 3(d) [5].
(a)
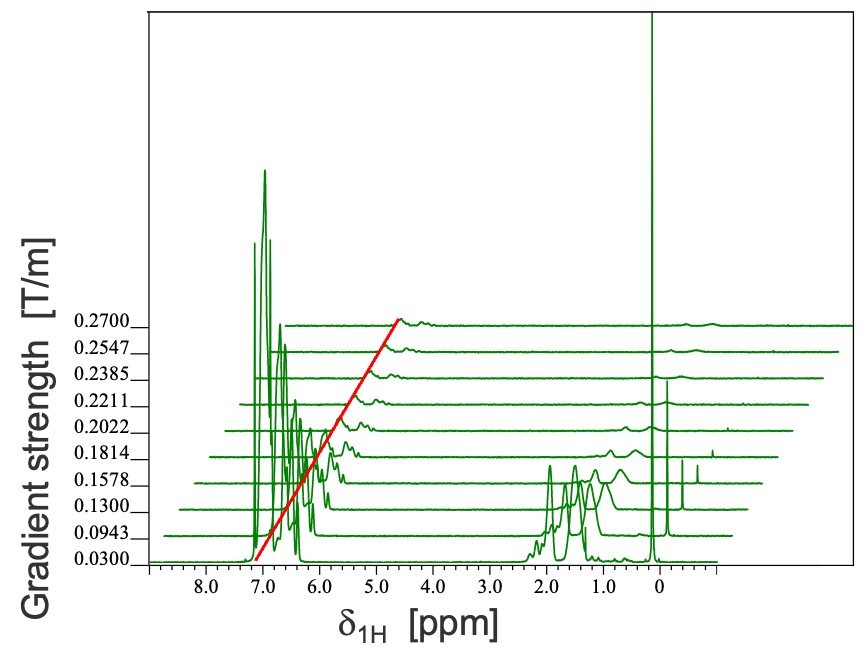
(b)
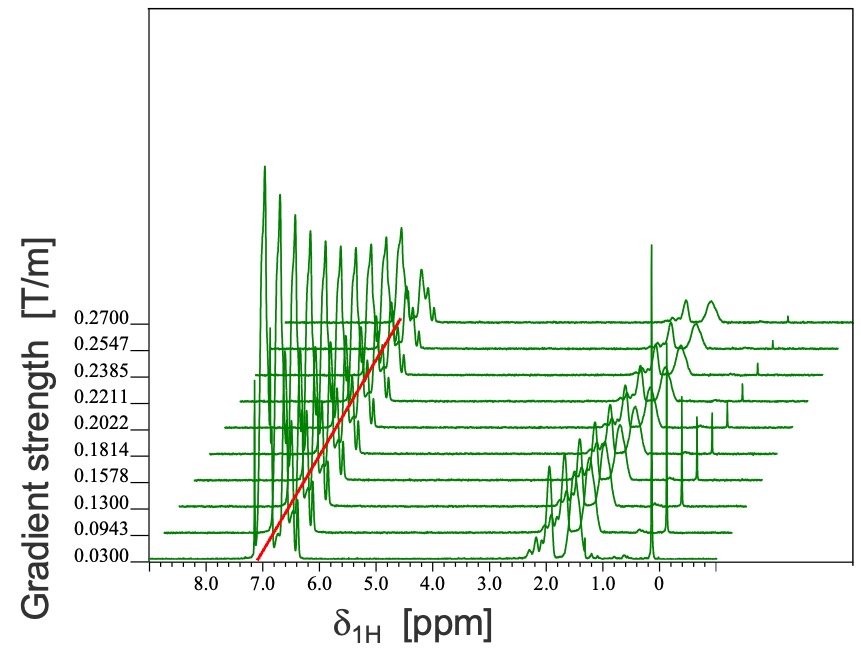
(c)
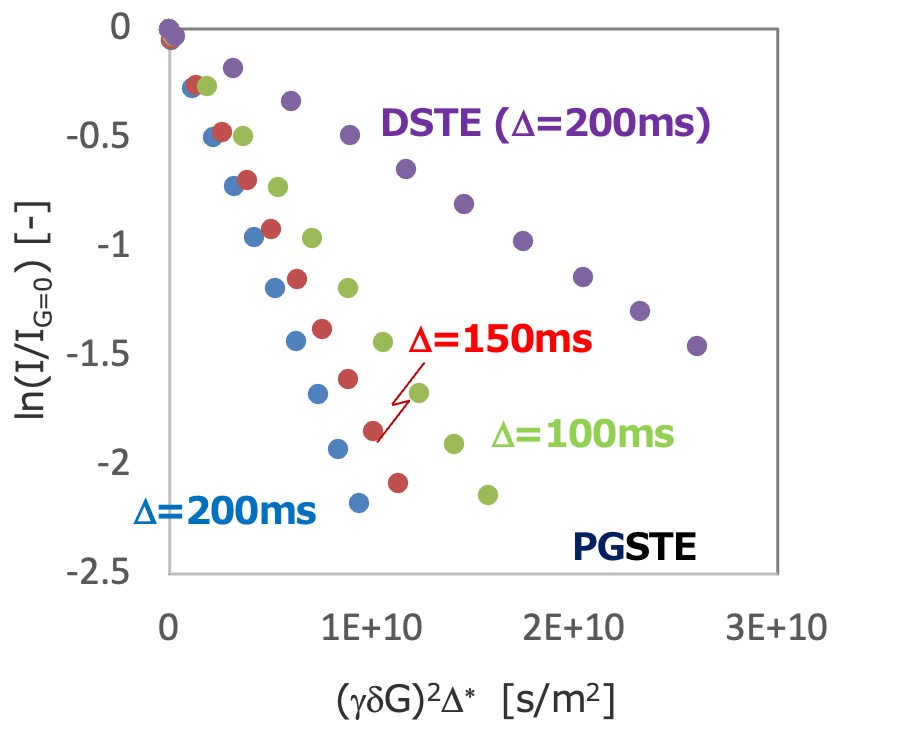
(d)
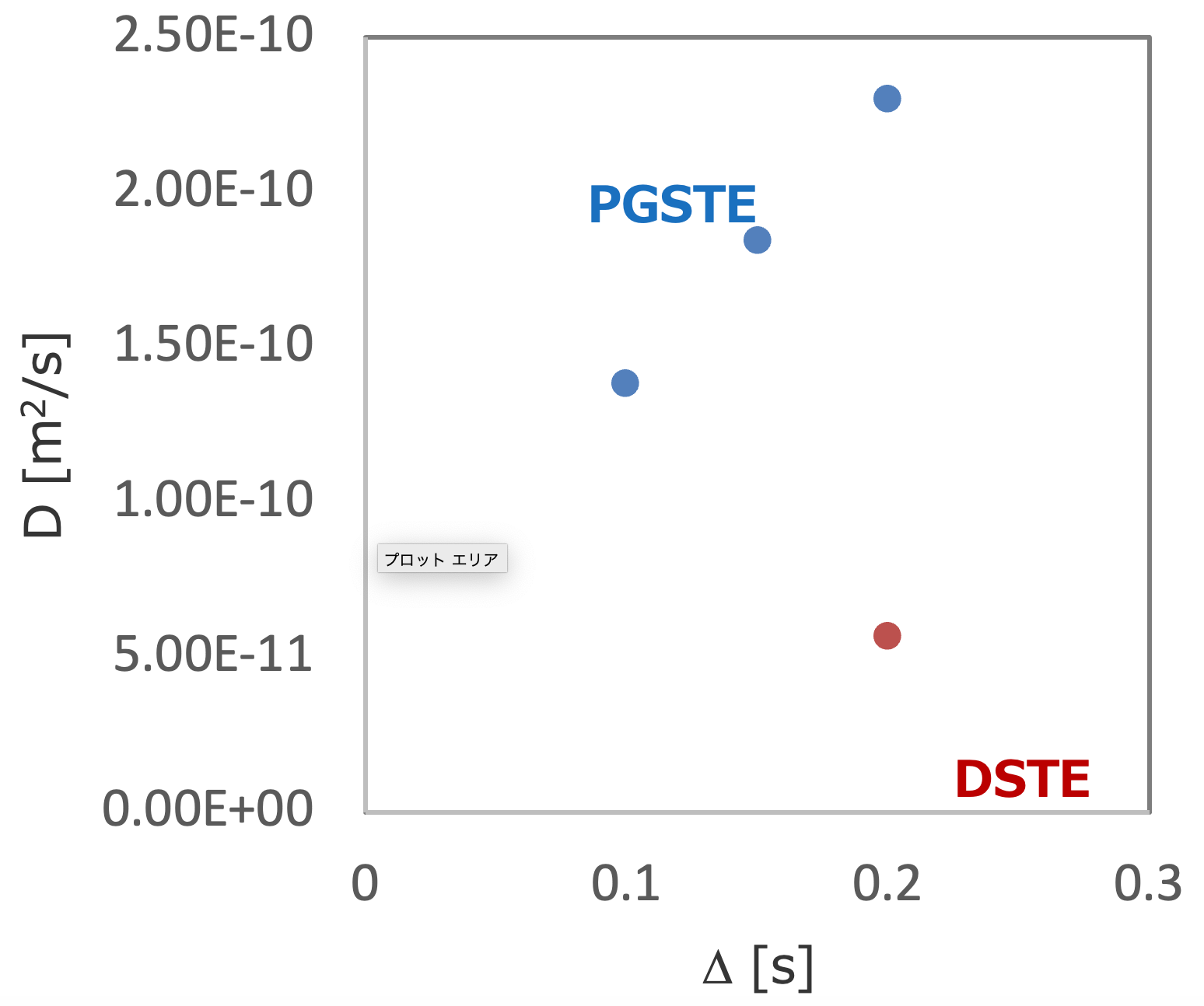
Figure 3 Comparisons between PGSTE and DSTE data of 4 w/v% polystyrene (31 kDa): arrayed (a) PGSTE data and (b) DSTE data.Despite utilizing the same experimental parameters in both the STE and DSTE experiments, the signal decay is faster in the STE experiment compared to the DSTE experiment. (c) The Stejskal-Tanner plot of signal decay at 6.96 ppm in the STE and DSTE experiments. (d) The ‘apparent’ self-diffusion coefficients exhibited proportionality to the diffusion times employed in the PGSTE experiments.
To conclude, DSTE offers a reliable solution for obtaining accurate self-diffusion coefficients even in the presence of thermal convection, effectively compensating for convection artifacts in the decay curve. This makes DSTE a powerful technique for PFG-NMR experiments conducted under high temperature or with low viscosity solutions. By comparing the self-diffusion coefficients obtained from PGSTE and DSTE, one can assess the impact of thermal convection on PFG-NMR experiments. The results presented here demonstrate the effectiveness of DSTE in mitigating the effects of thermal convection. Therefore, researchers may consider employing DSTE when conducting PFG-NMR experiments under similar conditions.
References
[1] Jerschow, A., Muller, N., “Suppression of Convection Artifacts in Stimulated-Echo Diffusion Experiments. Double-Stimulated-Echo Experiments” J. Magn. Reson., 125 (1997) 372-375.
[2] Stejskal, E.O., Tanner, J.E., “Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient”, J. Chem. Phys., 42 (1965) 288-292.
[3] Sinnaeve, D., “The Stejskal–Tanner Equation Generalized for Any Gradient Shape—An Overview of Most Pulse Sequences Measuring Free Diffusion” Concept. Magn. Reson., 40A (2012) 39-65.
[4] Claridge, T.D.W, “Diffusion NMR Spectroscopy” in High-resolution NMR techniques in organic chemistry 3rd edition, Amsterdam, Nederland: Elsevier B.V.
[5] Hedin, N., Yu, T. Y., Furó, I., “Growth of C12E8 Micelles with Increasing Temperature. A Convection-Compensated PGSE NMR Study” Langmuir, 16 (2000) 7548-7550.
Solutions by field
Related products
Are you a medical professional or personnel engaged in medical care?
No
Please be reminded that these pages are not intended to provide the general public with information about the products.

